The challenge task for the 1998 ICFP Functional Programming Contest consisted of a program for playing the game 'Pousse', or 'Push'.
The contest was announced on a Thursday evening and ran through the weekend. A single judge's prize, for the most thought-provoking entry, was awarded to the J Language team from Iverson Software, Inc.
The J entry consists of 113 lines of code (excluding comments and test code). A full screen interactive version contains 400 lines.
Pousse is played by two players X and O on an N x N board. Player X always moves first. A token may be entered from the left, the right, the top, or the bottom of the board, giving a total of N * 4 possible moves.
Placing a token onto the board causes all tokens in that row or column up to the first unoccupied cell to be shifted to make room for the new token. If the row or column is fully occupied, the last token is pushed off the board.
A row or column fully occupied by tokens of the same color is called a straight.
The game rules are:
- A player wins when he achieves a surplus of straights.
- A player loses if his move causes the board to re-enter a state which he caused earlier in the game.
- A player loses if he exceeds the time-limit on a turn.
Notwithstanding its simplicity, the playing strategy developed by the J team is surprisingly effective:
- On my turn, evaluate the boards resulting from my 4 * N moves.
- If all moves result in an immediate loss for me, select any one of those.
- Else if there are winning moves for me, select any one of those.
- Else select one of the moves which minimize the best counter-move of my opponent.
The K implementation of Pousse uses the J strategy.
The program supports two playing modes: interactive competition between a human player and a machine, and self-play, which pits the strategy against itself.
The K implementation (henceforth called 'push.k') consists of 92 lines of code. This comprises the playing logic and strategy (36 lines), as well as the global state (14 lines), GUI (13 lines), on-line help (22 lines), and run-time procedures (7 lines).
The script for push.k is divided into five main sections: the playing logic, the global state, the GUI, the on-line help text, and the procedures for initializing state when the script is loaded. These sections are separated by single blank lines.
It is convenient to begin with section 2, the global state.
The script is written to accept two optional command-line arguments: N, the number of cells along a side of the board, and T, the timeout value in seconds. The default values are N = 6, T = 30.
Following the empirical results obtained by the J team, the cells of an N x N board are weighted to the center. The variable D is recomputed whenever N is changed, and always has shape N x N. For N = 6:
D (1 2 3 3 2 1 2 3 4 4 3 2 3 4 5 5 4 3 3 4 5 5 4 3 2 3 4 4 3 2 1 2 3 3 2 1)
For an N x N board, the set of N * 4 valid moves is contained in M. For N = 3:
M ((`L;0) (`L;1) (`L;2) (`T;0) (`B;0) (`T;1) (`B;1) (`T;2) (`B;2) (`R;0) (`R;1) (`R;2))
A board is represented as an N x N character matrix. The board-history of a game containing k moves is represented as a (k+1) x N x N list H. Initially, H consists of a single empty board. For N = 3:
H
,(" "
" "
" ")
In the course of play, boards are appended to H.
The move-history of a game containing k moves is kept in a k x 2 list:
I
(("X"
(`B;1))
("O"
(`L;0))
("X"
(`B;1))
("O"
(`T;9))
("X"
(`B;1)))
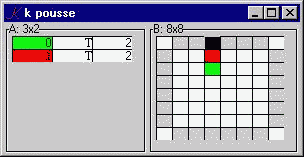
Move I[0] consisted of X playing (`B;1), and transformed the board from state H[0] to H[1]:
H[0 1]
((" "
" "
" ")
(" "
" "
" X "))
At the start of each game, the token of the machine is randomly selected and stored in P. In the game above, P = "X".
The variables W and O jointly represent the outcome of the game. Initially, they are W = " " and O = 0.
If X wins, then W = "X" and O = 1, and if X loses, then W = "X" and O = -1.
At the start of each turn, the global counter C is set to 0. Each second, a timer function fires which increments C and compares it to T, the timeout value. If T = C, the player of the turn loses.
The boolean global S is used to distinguish human-machine play (S = 0) and self-play (S = 1).
The variables E and R are used by the GUI (see below).
push.k uses K dependencies to keep global state and GUI self-consistent.
In general, there are two ways to keep GUI and global state consistent. In most programming environments, a procedural method is used: whenever any part of the state changes, invoke procedures to update the rest of the state and the GUI, and whenever any part of the GUI changes, invoke procedures to update the rest of the GUI and the state. The disadvantage of the procedural approach is that small changes to the system require changes to many procedures.
The alternative method uses dependencies: the state is defined as a functional dependency network, and the GUI is defined as a dependency on state. Whenever the root of the network changes, the rest of the network, including state and GUI, is invalidated; reference to any dependent component causes that component (and all components on which it depends) to re-evaluate.
The root of the push.k dependency network is N. All variables, including those which are mapped to the screen as constituents of the playing window, ultimately depend on the size of the board.
D, the weight matrix, is a function of N:
D..d:"weights N"
E, a list of indices into those edge positions of the board which accept click events, is a function of N:
E..d:"edges[-1_'1_'(N+2)_vs!_(N+2)^2]N+1"
M, the list of moves is a function of N and E.
M..d:"moves[N].'E"
R, a vector of indices into E which do not repeat previous states of the board, depends on H and M.
R..d:"nreps[H]M"
H, the board history, is reinitialized to ,(N,N)#" " whenever N changes.
H..d:",(N,N)#\" \""
P, the token assigned to the machine, is recomputed whenever N changes.
P..d:"N;piece[]"
I, W, C, S, and O, described above, are reset to constant values whenever N changes.
I..d:"N;()" W..d:"N;\" \"" C..d:"N;0" S..d:"N;0" O..d:"N;0"
Whenever N is reset, the global state (including the GUI variables described below) is invalidated. A trigger on N,
N..t:"hd[];sh[]"
causes the window to be hidden, and then shown.
hd:{`hide$`.k}
sh:{`show$`.k}
Showing the window causes the invalid global state to be recomputed to appropriate values, which in turn causes the window to be redrawn with correct size, color, and labels.
We step through the evaluation of two moves.
Begin by executing the niladic function 'play':
Z.play:{N::;if[P="X";me who[]]}
N is reset to its current value, invalidating all state variables and causing the playing window to be refreshed.
If P is "X", then the machine makes the first move. The niladic function 'who' returns the token of the current player. Since X always moves first, the token of the current player is simply the parity of the length of the board-history H:
who:{"OX"(#H)!2}
If the game is not over, then initialize the timer counter C, and call 'go' with token x and the move computed by the strategy function 'str'.
me:{if[~O;C::0;go[x]str[x;*|H]]}
'str' takes two arguments: token x and the current state of the board (the last item in H):
str:{:[#R;ev2[x;move[x;y]'M R];*M]}
If there are moves which do not repeat the previous state of the board -- that is, if 0 < #R -- then call 'ev2' to select from the space of possible moves, else return the first move. Observe that if no non-repeating moves are available, the game is lost: *M is no worse than any other move.
'ev2' takes two arguments: token x, and a list of the boards which result from x applying a non-repeating move to board y.
First we look at 'move' and its subfunctions.
'move' takes token x, board y, and move-instruction z and returns the result of applying (x;z) to y.
move:{F[*z;1]@[F[*z;0]y;z 1;push[x]]}
push:{x,y _di(-1+#y)&y?" "}
F[`T`R`L`B]:((+:;+:);(|:';|:');(::;::);(|:'+:;+|:'))
z has the form (f;n), where f is `L, `R, `T, or `B, and n is in 0 ... N-1. Suppose that f is `L and the nth row of board y is
"XXO X "
Then if x is "X", the result of applying move (f;n) to board y is
"XXXOX"
Alternatively, suppose that the nth row of y is
"XXOOXO"
Then the result is:
"XXXOOX"
Rather than write four special cases to deal with left, right, top, and bottom token-insertion, 'move' transforms the board so that 'push' can treat any move as an insertion from the left, then applies the reverse transformation to the result. The four pairs of transformations are stored in the dictionary F. For example, suppose that f is `T. Then F[f] is (+:;+:). F[f;0] transposes the board, putting the top of y on the left:
y ("XOX" " XO" " ")F[`T;0]y ("X " "OX " "XO ")
and F[f;1] undoes the transformation.
The way to read
F[*z;1]@[F[*z;0]y;z 1;push[x]]
is:
apply F[*z;1] to: the result of applying push[x] to: the z 1-th row of the result of applying F[*z;0] to: y
The 'push' function prepends token x to row y from which we remove either the first blank (case 1 above) or the last token (case 2 above). That is, we read
x,y _di(-1+#y)&y?" "
as: x joined with y without the index of the minimum of the last position and the index of the first blank.
Now we can return to 'ev2'.
ev2:{any@:[#i:&0<x evs'y;i;mmx opp[x]ev''y move[opp x]/:\:M]}
mmx:{&(&/m)=m:|/'x}
any:{M R x()_draw#x}
x is the current token and y is a list of boards. 'ev2' applies 'any' to the result of a conditional of the form
:[a;b;c]
In the condition, we check to see whether any of the boards contain an immediate win for x. That is, we see whether 0 < #i, where i contains the indices of the boards which contain a surplus of straights for x. If there are winning moves, the conditional returns them to 'any', which selects one randomly, and indexes out the corresponding non-repeating move. If there are no winning moves for x, then we compute a matrix of boards for opp[x], the opponent of x. Each row consists of a list of those boards which opp[x] can reach from one of x's boards by applying M. Then we evaluate each one of those boards from opp[x]'s perspective, and minimax the resulting scores.
'str' is called by 'me' and returns the selected move to 'go':
me:{if[~O;C::0;go[x]str[x;*|H]]}
go:{I,:,(x;y);*|H,:,move[x;*|H]y;chk x}
'go' appends the selected move to I, applies it to the current board, and appends that to H, giving a new current board. It then calls 'chk' to see if x has won or lost the game:
chk:{:[evr[-1+#H;x;*|H];end[x;-1];evs[x;*|H];end[x]1]}
'chk' is a conditional of the form
:[a;b;c;d]
If x has repeated a previous board which he caused, x loses, else if x has a surplus of straights, x wins.
The 'end' function is simple:
end:{W::x;O::y}
W is the token of the player who ended the game, O is how he ended it: 1 if x won, -1 if x lost.
'evr' and 'evs' are evaluation functions. There are four of them:
evc:{-/(+//D*)'y=/:x,opp x}
evs:{-/{+/(&/+x)+&/x}'y=/:x,opp x}
evr:{-z _in H@&("X"=y)=(!x)!2}
evl:{+/pow@,/(+/';+/)@\:0 1 -1(" ",x,opp x)?/:/:y}
'evc' returns the difference in weighted counts of x and opp[x]. Intuitively, it reflects 'control of the center'.
'evs' returns the difference in straights of x and opp[x]. Any positive number represents a win for x.
'evr' returns -1 if board z repeats a board caused by player y. -1 represents a loss for x.
'evl' returns a score based on the number and lengths of partial straights for player x. Intuitively, x is ahead of his opponent if he has more and longer partial straights.
The master evaluation function is
ev:{evl[x;y]+evc[x;y]+1e8*evr[#H;x;y]+evs[x]y}
If the move results in a surplus of straights, then 'evr' must return 0. If the move results in a repeated board, then 'evs' must return 0. If the move is not an immediate winner or an immediate loser, then straights + repeats must be 0. So 1e8 * the sum of the repeat and straight scores will either be 0 or dominate the calculation.
The overall score is therefore either a very large positive number (immediate win), a very large negative number (immediate loss), or the sum of the differences in partial straights and the differences in control of the center of the board.
This scoring method was developed by the J team for their contest entry.
The game alternates between you and me until one of us wins or loses:
you:{if[~O;C::0;go[who[]]x;me who[]]}
me:{if[~O;C::0;go[x]str[x;*|H]]}
or a timeout occurs:
time:{if[~O;:[S;me who[];T=C+:1;end[who[];-1]]]}
The 'time' function checks to see if the game is over. If not, then if we are in 'selfplay' mode (S = 1), we play immediately. If we are in 'play' mode, then if the current player has reached the timeout value, the current player loses.
In 'selfplay' mode, the state is re-initialized, S is set to 1, and the machine makes the first move. Subsequent moves are made each second, until the game is over.
Z.self:{N::;S::1;me who[]}
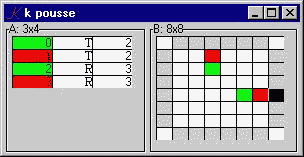
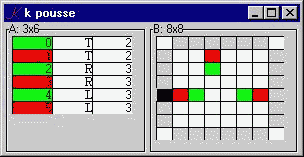
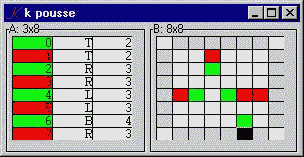
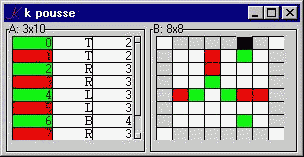
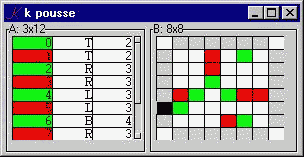
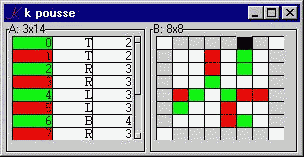
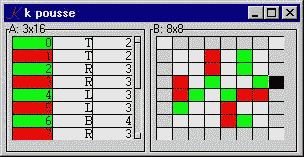
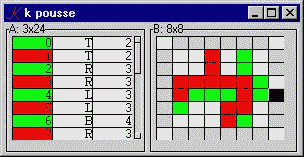
The Pousse GUI consists of a form, .k, with two components: A, the moves so far, and B, the current state of the board. We look first at B.
B..d:"board@*|H"
B depends on the current board, the last element of the board history H. The 'board' function returns the current board, surrounded by blanks. The edges of the result will be used to accept click-events, which trigger the corresponding moves.
board:{,:''(-n+1)$n$+(-n+1)$(n:1+#*x)$x}
For example, where '.' represents a blank, if the current board is
.X.O
..OX
.X..
...O
then the screen representation should be
......
..X.O.
...OX.
..X...
....O.
......
Here is the representation with '+' for those edges which correspond to moves:
.++++.
+.X.O+
+..OX+
+.X..+
+...O+
.++++.
Since K displays matrices in transposed form, the 'board' function returns its result in transposed form.
In order to force each cell of the board to appear in its own box, the function enlists each cell of the matrix with ,:''. Hence, the result of 'board' is a matrix of one-element character vectors.
B..k:"if[_i _in E R;you M E?_i]"
When the player clicks on a cell, the click action checks whether the position corresponds to a non-repeating move. If it does, the action calls 'you' with the corresponding move from M.
B..bg:{:[_i _in E R;808080;999999 990000 9900(" ",P)?*B ._i]}
The background color attribute is a conditional: if _i is a non-repeating move, then we color the cell light gray (808080), else we color it white (999999) if the cell is unoccupied, red (990000) if it's occupied by me, or green (9900) if it's occupied by you.
B..fg:{:[_i _in E R;0;999999]}
The foreground color attribute is also a conditional: if _i is a non-repeating move, the foreground color is black, else it is white. Hence, when the user clicks on a cell, it turns black if the click causes a move, white if it does not.
The rules of Pousse state that a player loses if his move repeats a previous state of the board which he caused. As the game proceeds, the machine's advantage over its human opponent increases. To keep the game interesting, R -- an index into those moves which do not repeat a previous state -- is calculated at each turn and used to alert the human player to losing moves. This is done by (i) making the foreground of a losing edge-cell go white instead of black on a click, and (ii) not acting on clicks to those cells.
B..f:" "
Finally, because we are using "X" and "O" as our tokens, but representing them with red and green, we format every cell as a constant blank.
The move history A is also a dependency:
A..d:"+$,/'I"
We raze each move, format, then transpose the whole for display. For example, if I 0 is a move
("X";(`L;3))
then $,/I 0 is
(,"X";,"L";,"3)
We supply a formatter for A:
A..f:{:[x~_n;14$" ";*_i;4$x;4$_i 1]}
If the move history is empty, then we return 14 blanks to keep the display stable. Else, if we are formatting the second or third positions, we return the value formatted for 4 positions. Else we return the index of the move formatted in 4 places.
Background coloring correlates each move with the player who made it:
A..bg:{:[~*_i;9900 990000 P=*x]}
If we are coloring the token (which we have formatted as a blank), then we use red if the token = P, else green.
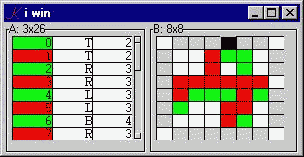
If the game is over, we can retrieve the board corresponding to any move of the previous game by clicking on that row of A:
A..k:"if[O;R:nreps[(2+_i 1)#H]M;B:board H 1+_i 1]"
That is, if O is not 0, then we compute R, the indices of the non-repeating moves, and assign to B the 'board' of the corresponding element of the board history H. In the course of normal play, R and B are recomputed automatically, since they are on-screen dependencies. In A..k, we recompute them explicitly.
Finally, we add the necessary attributes to .k to configure it as a form:
.k..c:`form .k..a:,`A`B .k..l..d:".k.over[.k.W].k.O"
The last line is interesting. Here, we define the label of the form as a dependency. When the game is over, W and O are assigned by the 'end' function. The label of the form re-evaluates to report the result:
over:{:[y;($`you`i P=x)," ",$`lose`win y=1;"k pousse"]}
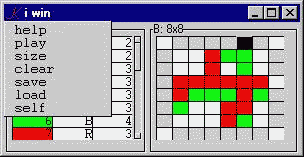
We attach options to the form by defining the label-click of the window as the niladic function 'menu':
.k..kl:".k.menu[]"
menu:{{if[~_n~x;Z[x][]]}@`4:`menu,,!Z}
If the user picks one of the options in the menu list, we run the corresponding niladic function in the directory Z. This is a convenient way to add and remove active elements in a menu, since !Z, a vector of symbols of the functions in Z, serves both as the parameter to the menu call and a vector of possible indices into the executable function dictionary Z. Note in particular that 'size' is:
Z.size:{if[~_n~r:`4:`menu,,`$$6+!15;N::0$$r;play[]]}
'size' is a submenu, where the user can reassign N, the boardsize. As we have seen, both the global state and the GUI depend on N, so this causes Pousse to be reinitialized and placed in 'play' state.
Other options are: save a game to disk, load and replay a game on disk, and clear the current game.
When push.k is loaded, the functions and global variables are defined, and the GUI attributes are assigned. The final lines of the script set the random seed to the current time, set the timer to fire every second, attach the timeout function to the timer trigger, show the window (thus forcing validation of all dependencies), and enter 'play' mode:
."\\r ",$_t \t 1 .t..t:".k.time[]" sh[] Z.play[]
K has been designed to maximize both productivity and performance. We are used to seeing it deployed on problems involving large data or complex calculations. Since the ICFP challenge problem uses small data and simple calculations, the K solution concentrates on maximizing productivity. This is achieved by exploiting two features of the K language:
First, it is a straightforward matter to map the logic of the game onto simple, easy-to-understand functions. For example, 'move' takes a player's token x, a board y, and a move z, and returns the board which results from x playing z on y.
Second, the GUI is easy to define as a two-way transformation of the global state used by the game logic: a mapping from internal state to screen variables and their attributes, construed as functions, and a mapping from click events on those screen variables to function calls which modify state.
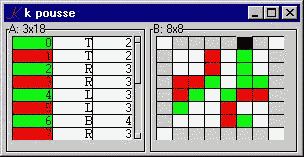
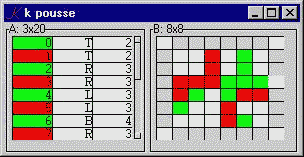
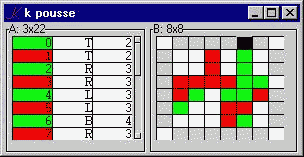
A small game:















* Thanks to Jan Karman and Mike Rosenberg for suggestions.
Stevan Apter
31.July.1999